1638年,举世闻名的意大利科学家伽里略出版了世界上第一本材料力学教本《两种新的科学》,首次提出了材料的力学性质和强度计算的方法,标志着材料力学这门学科的开端。同时伽利略也是现代实验力学的奠基人,他最早在材料力学中提出了实验观察和理论推导相结合的方法研究了梁的弯曲强度问题。虽然伽利略在研究梁弯曲强度时没有考虑材料的变形,得出的梁横截面上弯曲应力分布的研究结论也是错误的,但他的研究方法和研究的问题引导了后继的科学家,不断完善了梁理论的研究。另外,伽利略还研究了直杆的轴向拉伸问题,并得到了承载能力与横截面成正比而与长度无关的正确结论。当时他虽对于一些杆、梁(多是脆性材料制成的)进行了很多试验和计算,但是他未能确切地提出应力的概念。后来,由于生产力和科学技术的进一步发展,直到1822年法国科学家柯西(Cauchy)才明确地提出应力和应变的概念。

图1 伽利略

图2 悬臂梁应力试验
几乎比伽里略早一个世纪,文艺复兴时期的意大利美术大师达·芬奇(1452~1519)最早利用实验手段研究了材料的强度问题。在大家的印象中,提起达芬奇,首先会想到他的名画《蒙娜丽莎的微笑》、《最后的晚餐》等,实际上达芬奇的成就远不只是画作,他在几乎你能够想到的所有领域都有显著的成就。他的研究成果大多没有正式发表,都保存在他的手稿中。作为画家,达芬奇完成的画必须悬挂起来让人欣赏,当时就有一些挂画的铁丝发生断裂的现象,就这样他对铁丝的断裂特性产生了浓厚的兴趣。为了研究铁丝的断裂强度,达芬奇设计了图中所示的试验方案。并得出了长铁丝比短铁丝更容易发生断裂的结论。根据现代材料力学的基本理论,铁丝的强度与长度无关,但如果根据现代断裂力学理论,抛弃材料力学基本假设,这一结论无疑是合理的。达芬奇还系统研究了梁的强度问题,并得到了一个普遍性的原理:任何被支撑而能自由弯曲的物件,如果截面和材料都均匀,则距支点最远处,其弯曲也最大。达芬奇建议了一系列有关梁的试验。如对于简支梁,他研究了梁的长度和宽度对梁承载能力的试验。他的结论是:简支梁的强度与其长度成反比而与其宽度成正比。在达芬奇的手稿中,还可以发现一些有关立柱强度的研究,他说明了柱(压杆)的强度是和其长度成反比而与其横截面的某些高宽比成正比。达芬奇的这一结论很可能已经意识到了压杆失稳问题,某些高宽比,可能就是说明压杆强度需要寻找最小惯性矩。而“强度与长度成反比”是错误的,应该是与长度的平方成反比。

图3 达芬奇

图4 达芬奇设计的铁链受拉试验
1502年,达芬奇想出了一种新颖的桥梁设计,他在给苏丹的一封信中对它进行了描述,结构如图所示。达芬奇提出了桥台向两边展开的设计方案来防止横向运动,横向运动导致了几个世纪以来许多桥梁的倒塌。这座桥原本约为366m长,24m宽,如果建成的话,将成为当时世界上跨度最长的桥,其跨度几乎是当时普通桥梁的10倍。巴耶塞特二世认为无法建设如此大跨度的桥梁而未能施行。1996年,挪威艺术家威卜琼·山得(Vebjørn Sand)看到达芬奇的设计后,就希望能够将其变成现实。2001年,世界首座达芬奇桥梁诞生了,结构如下图所示,此后世界各地陆续建成了其它的达芬奇桥梁。由以上达芬奇的力学成就可知,他也许是世界上最先试图用静力学来求,作用在某些构件上的力的人,同时也是最先用实验来决定结构材料强度的人。可是,这些重要的倡导一直被埋没在他的笔记里,而在十五及十六世纪的工程师们却和罗马时代一样,继续地仅凭经验和武断来决定构件的尺寸。

图5 达芬奇的单拱桥

图6 挪威达芬奇大桥(人行桥)
下面我们接着讨论胡克在材料力学方面的贡献。胡克于1687年曾将自己发现的弹性定律发表在他的演讲集《态势的恢复》中,他举出螺旋弹簧、发条、悬线和木杆挠曲变形等四种情况,建立了弹性体变形与力成正比的定律,即胡克定律。此图所示为虎克实验用装置,虎克发现,杆或弹簧在拉力作用下,伸长量与拉力成正比。后来,法国科学家泊松在1829年发表的《弹性体平衡和运动研究报告》中进一步推广了应力和应变关系,推演出弹性杆在受到纵向拉伸时,横向收缩应变与纵向伸长应变之比是一常数,即材料的泊松比。另外,胡克还同惠更斯各自独立发现了螺旋弹簧的振动周期的等时性等,从而为机械式时钟的发明提供了理论基础。胡克在做木杆的弯曲变形时,得出杆的一侧纤维伸长,而另一侧压缩,中间某层纤维不变形(即中性层),得出梁横截面上的应力分布应当是,以梁横截面上中性层为0的线性分布,但胡克并没有进一步的展开。胡克虽擅长于实验技术且物理思想活跃,但由于缺乏数学根基,最终未能从理论和实验上根本解决问题。

图7 胡可

图8 胡可定律试验
17世纪马里沃特(Mariotte 1620~1680)作了木材的拉伸实验,并已开始研究梁的弯曲实验。马里沃特是法国实验物理学的创始人,他的空气实验归结为有名的波义尔-马里沃特定律;在固体力学方面,马里沃特创立了冲击定理,他利用悬挂在绳索上的小球来说明动量定律,并发明了冲击摆。马里沃特在一篇流体运动的论文里,包括了他对材料力学方面的研究。他曾设计过通向凡尔赛宫的一条供水管线,设计的结果使他对于梁的弯曲强度发生了兴趣。利用木材和玻璃杆做实验,他发现伽利略理论所得的断裂荷载值过大,为此他提出了自己的弯曲理论,在他的理论中已将材料的变形考虑在内。在马里沃特的分析中,他在弹性梁内所采用的应力分布理论上是适当的,他关于纤维中应力分布的假设也是正确的。不过在计算图中I点的拉力力矩时出现了错误,导致马里沃特无法得出梁在弹性范围内的正确强度公式。在这里我们看到,马里沃特大大地丰富了材料力学理论。由于提出了考虑弹性变形的结果,他改进了梁的弯曲理论,并利用实验来校核他的假说。
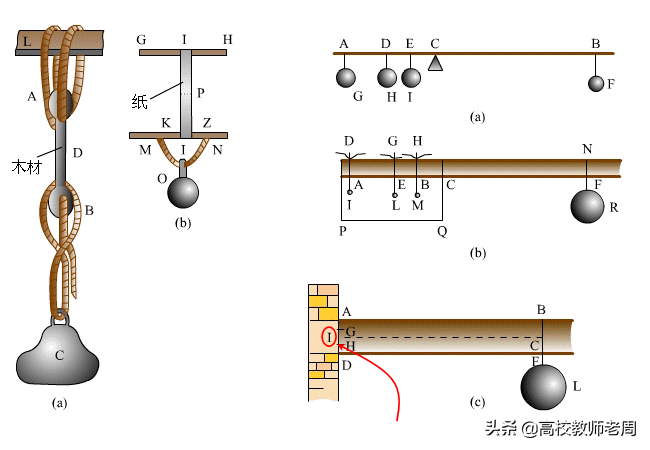
图9 马里沃特的实验
十七世纪的最后二十五年到十八世纪的初期,微积分学开始迅速发展。瑞士数学家和力学家雅克比伯努利,在1694年出版的《弹性梁的弯曲》中最早用微积分工具研究了梁的变形,得出悬臂梁变形的微分方程,指出了梁挠曲线上每一点的曲率与该点处的弯矩成正比这一正确结论。从此开创了材料力学中重要一章。其实伽利略和马里沃特只研究了梁的强度,而雅克比伯努利却做出了梁的挠度计算,他并没有对我们贡献材料力学性能方面的知识。另外,雅克比伯努利在研究梁的变形过程中提出了平面假设,即梁的横截面在变形前后始终保持为平面。平面假设在材料力学中具有十分重要的地位,是否采用平面假设,也是材料力学与弹性力学的主要区别之一。值得注意的是,雅克比伯努利在研究梁的弯曲时,假设下边缘不变形,因而中性轴的位置是错误的。后来,欧拉继续雅克比伯努利的工作,在1744年建立了梁的挠曲线方程,完成了梁的弯曲理论。后来凡是采用平面假设的梁我们也称为欧拉-伯努利梁,以纪念这两位科学家在梁弯曲理论的贡献。现在我们材料力学教材上研究的梁就是欧拉-伯努利梁。

图10 雅克布.伯努利
欧拉是瑞士数学家,他还是弹性系统稳定性理论的开创人。欧拉在材料力学方面的贡献主要是,利用微积分研究了梁的挠曲线方程和弹性压杆的稳定性问题。早在文艺复兴时期,达·芬奇对弹性压杆做了一些开拓性的研究工作。荷兰物理学家穆申布罗克于1729年通过对于木杆的受压实验,得出“压曲载荷与杆长的平方成反比的重要结论”。随后,欧拉在1744年出版的变分法专著中,得到细长压杆失稳后弹性曲线的精确描述,及压曲载荷的计算公式。而材料力学教材中两端铰支压杆压曲载荷公式是拉格朗日在欧拉近似微分方程的基础上于1770年左右得到的。

图11 欧拉
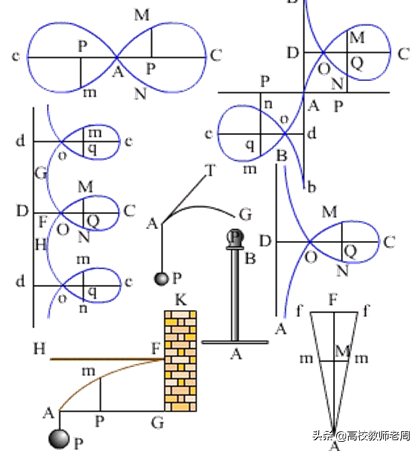
图12 欧拉研究的弹性曲线
十八世纪时期的科学家们对于材料力学的成就,没有人比得上库伦。库伦是18世纪法国杰出的物理学家和军事工程师,众所周知,库伦电磁学研究成果具有划时代意义。然而,鲜为人知的是,库伦早在从事电磁学研究之前,已经在建筑力学、材料力学和摩擦理论作出了许多重要贡献,并以此当选为法国科学院院士。库伦对材料力学的最主要贡献包括梁的理论和扭转理论。关于梁的理论,通过前面的介绍,早在17世纪的伽利略、马里沃特以及18世纪的雅克比伯努利和欧拉等人均在梁的理论上取得了相当的进展,但由于他们均未考虑梁的受压区域的变形,即应力与应变成正比,因而最终未能圆满地解决这个问题。库伦在1773年的论文《梁的弯曲问题》中,率先对作用集中力的悬臂梁的横截面上的力作了合理的全面讨论,纠正了伽利略、马里沃特和伯努利等人著作中的错误,在考虑完全弹性的情况下,横截面上存在受压区和受拉区,中间则存在一个变形前后纤维长度不变的中性层,并把截面上的力与一侧的外荷载建立了完美的平衡关系。同时,库伦还提出了一个重要而又新颖的见解,即切应力对一根中空长梁的挠曲没有显著作用,这在今天的日常生活、建筑工程及工业生产上都有广泛的应用。关于扭转理论,库伦的第一篇关于扭转理论的论文《关于制造磁罗盘的最佳方法研究》中描述了丝线和发丝的扭转实验,证实了扭力与扭转角成正比这一正确结论。1784年库伦向法国科学院提交的《金属丝弹性和扭转力的理论和实验》论文中,给出了扭摆微分振动方程和周期,并指出扭矩与转角、金属丝直径和长度之间的关系。库伦正是在这种扭转理论的基础上,制成了扭秤,如图所示,并进行了著名的扭秤实验,从而建立了库伦定律。此外,库伦还通过扭转实验,发现了塑性材料的冷作硬化现象,借冷作或淬火方法,提高材料的弹性极限。后来法国力学家圣维南(Saint-Venant)于19世纪中叶运用弹性力学方法奠定了柱体扭转理论研究的基础。

图13 库伦
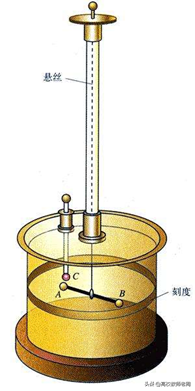
图14 库伦扭称
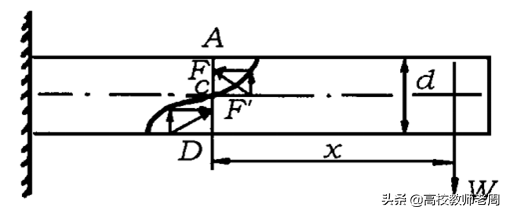
图15 库伦的梁理论
库伦虽然指出了中性层,但他没有给出中性层的具体位置,因而也没有得出弯曲正应力的正确计算表达式。材料力学关于梁的强度理论中更进一步的发展应归功于纳维。纳维于1826年在所著《力学在机械与结构方面的应用》中系统讲述了材料力学的第一本书,第一次给出中性层的准确定义,即当材料服从胡克定律时,中性层必通过横截面的形心。由此得到了纯弯曲横截面上正应力的正确计算公式。在纳维所著的《材料力学》这本书的头两节,作者还讨论了棱柱杆的简单受拉和简单受压,并指出,要说明某一材料的特性,仅得到它的强度是不够的,还必须表明它的弹性模量E。此外,纳维是第一个发明出用三关系法分析材料力学中超静定问题的人,即在分析变形体或弹性体的超静定问题时,在静力学方程以外,引入表示变形协调条件的方程式,进而解决所有的未知量。

图16 纳维
托马斯.杨是英国医生、物理学家、光的波动学说的奠基人之一。他不仅在物理学领域名享世界,而且在材料力学方面也颇有建树。杨在1807年首次定义了材料在拉伸和压缩时的杨氏弹性模量。杨氏模量的引入曾被英国力学家乐甫誉为科学史上的一个新纪元。杨认识到剪切是一种弹性变形,称之为横推量,并注意到材料对剪切的抗力不同于材料对拉伸或压缩的抗力,但他没有引进不同的刚度模量来表示材料对剪切的抵抗。此外,他对材料的扭转、偏心拉压等问题也有研究。

图17 托马斯杨

图18 杨氏模量E
任何一门科学都不可能是在短期内创造出来的,而是经过几代人艰苦探索和创造而逐渐形成的。此后法国的科学家泊松、圣维南、柯西和拉梅,德国科学家摩尔,俄国工程师儒拉夫斯基和别斯帕罗夫等等都对弯曲理论、扭转理论、稳定理论以及材料实验作出卓越的贡献,丰富、发展和完善了材料力学这门学科,他们对科学的献身精神为后人所敬仰。
20世纪以来,铁路、桥梁的发展以及钢铁和其他新材料的出现,使得力学的分工越来越细,出现了更多的以材料力学、结构力学、弹性力学为基础的固体力学分支,例如计算力学,断裂力学,粘弹性力学,复合材料力学,实验固体力学等等。而这些学科的发展反过来促进了航空航天,工程机械、石油勘探,喷气技术,大型水利工程等一系列力学问题的解决。
